Você já foi “passado para trás” por algum colega de trabalho ou por seu superior? Já obteve vantagens sobre outras pessoas e depois pagou por isso? A Teoria dos jogos explica.
Quem teve a oportunidade de assistir ao filme “Uma Mente Brilhante”, ganhador de vários prêmios no Oscar de 2002, teve a oportunidade de conhecer um pouco sobre o matemático John Forbes Nash Jr. Muito mais interessante que sua esquizofrenia ou seu casamento, o trabalho de Nash foi revolucionário e até hoje é polêmico.
Nash trabalhou sobre o que ficou conhecido como “Teoria dos Jogos”. Esta teoria matemática foi concebida em 1944 por dois outros matemáticos: Oskar Morgenstern e John von Neumann; este último famoso por ter sido um dos pais da bomba atômica e do computador digital.
O que Nash fez de realmente notável foi expandir esses conceitos puramente matemáticos para o mundo do comportamento humano – economia, sociologia, antropologia e biologia.
Conheça nossas oficinas presenciais com gamificação aqui.
Do que se trata a Teoria dos Jogos?
De forma simplificada, com essa teoria, pretende-se responder à seguinte pergunta: “O que é mais vantajoso para mim, sabendo que a minha decisão vai implicar em uma reação da(s) outra(s) parte(s): cooperar (agir colaborativamente) ou desertar (tomar uma decisão egoísta)?”
Traduzindo a pergunta para o ambiente das organizações, ela poderia ser feita mais ou menos assim: O que vale mais a pena: conseguir uma vantagem muito alta hoje sobre um colaborador / colega de trabalho / fornecedor OU tentar uma opção em que ambas as partes ganhem menos agora para continuar se relacionando e gerando resultados positivos no futuro?
Se você tem interesse em conhecer mais sobre mecânicas da gamificação que tratam de cooperação e competição, baixe nosso livro ligital sobre o assunto.
A teoria dos jogos é mais facilmente explicada usando do Dilema do Prisioneiro, jogo que explicaremos abaixo.
Conheça nosso catálogo de cursos
de habilidades do futuro aqui.
O Dilema do prisioneiro
O Dilema do Prisioneiro mostra a seguinte situação: existem dois comparsas (Barbicha e Ruivo) que cometeram grandes crimes no passado, e a polícia nunca conseguiu pegá-los. Em uma oportunidade, eles são pegos cometendo um crime pequeno.
Ao serem interrogados, são colocados em salas separadas. Três opções de decisão, juntamente com três consequências, são colocadas para cada um deles:
- Se nenhum dos dois confessar, ou seja, um coopera com o outro, cada um deles pode ser condenado a 6 meses de prisão – pelo crime pequeno que cometeram.
- Se apenas um acusa o outro dos crimes passados (confessa), o desertor que acusou o amigo sai livre. O acusado, que cooperou com o amigo, é condenado em 10 anos de prisão.
- Se ambos confessarem, ou seja, um acusa o outro pelos crimes anteriores, ambos pegam 5 anos de prisão.
A imagem abaixo esquematiza as decisões. As decisões são simultâneas e um não sabe nada sobre a decisão que o outro vai tomar.
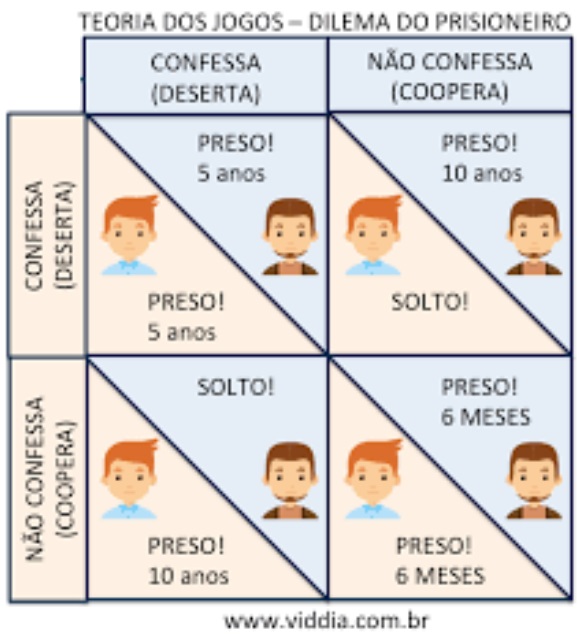
Esse dilema mostra que cada prisioneiro pode satisfazer o seu próprio interesse (desertar) ou atender ao interesse de ambos (cooperar).
Acontece que Ruivo pensa da seguinte forma: “Vou admitir que Barbicha vai cooperar comigo ficando quieto. Neste caso, se eu cooperar também, ficarei 6 meses preso, o que é um bom resultado.
Mas se ele cooperar e eu trair confessando o crime, eu saio livre, que é o melhor resultado possível! Porém, se Barbicha desertar e eu continuar cooperando, sou eu que ficarei 10 anos na cadeia, que é o pior resultado possível, e ele sai livre.
Mas se nós dois desertarmos, eu ficarei somente 5 anos preso (um resultado intermediário). Eu concluo então que, em ambos os casos (se ele cooperar ou não), sempre será melhor desertar, e é o que eu vou fazer.” Barbicha pensa da mesma forma e ambos acabam desertando.
Por que cooperar vale a pena
Na situação acima, se ambos cooperassem, haveria um ganho maior para os dois, mas a otimização dos resultados não é o que acontece. Ao invés de ficarem somente 6 meses presos, eles passarão 5 anos na cadeia para evitar o risco de ficar 10 anos se o outro optar por desertar. Mais que isso: desertando, cada parte tem a possibilidade de sair livre se a outra parte cooperar!
Segundo o conceito original da Teoria dos Jogos, a deserção seria a alternativa racional, porém, em um jogo de rodada única. Mas na vida real e nas organizações, o que acontece com maior frequência são situações de repetição do jogo, onde a cooperação mútua tende a trazer os melhores resultados tanto individual quanto coletivamente.
Vamos pensar de maneira simplificada para facilitar o raciocínio: se o jogo acima se repetisse por 10 vezes e, em todas elas, ambos desertassem, eles ficariam presos 10 x 5 anos = 50 anos. Se, nas 10 vezes, ambos cooperassem, ambos ficariam presos 10 x 6 meses = 60 meses = 5 anos!
E, mais importante, não existe a possibilidade de apenas um deles desertar em todas as vezes, pois a partir do momento em que um deserta na primeira vez, não existe mais confiança nas próximas rodadas. Logo, a situação ganha-perde pode acontecer apenas na primeira rodada. A partir do momento que uma das partes sentiu que perdeu, ele fará de tudo para “descontar” em alguma oportunidade futura!
Trazendo a teoria dos jogos para e relacionamento interpessoal, é importante que as decisões tomadas promovam, legitimamente, ganhos para todos. Pela teoria dos jogos, é provado matematicamente que, a longo prazo, é a melhor opção.
A base de tudo
Nos grupos humanos em geral é essencial que se possa acreditar que cada membro irá se comportar cooperativamente. É a base de um conceito que costumamos chamar de confiança. Se todos tiverem a certeza que todos cooperam, será muito melhor o desempenho do grupo como um todo.
O grande problema é convencer cada um dos componentes do grupo a cooperar mesmo em situações em que a deserção traz o melhor resultado individual imediato. Por isso foi necessário criar mecanismos de punição, em que o indivíduo não-cooperativo é penalizado, seja com multas, ou parando de se relacionar com esse tipo de indivíduo.
Referência: MARINHO, Raul. Prática na Teoria: aplicações da teoria dos jogos e da evolução aos negócios, São Paulo: Saraiva, 2005.null
Saiba mais
Criamos cursos, oficinas e treinamentos das principais habilidades do futuro: auto eficácia (inteligência emocional, solução de problemas e mentalidade ágil), habilidades interpessoais (comunicação, escuta ativa, empatia e influência) e habilidades de gestão (liderança, gestão de projetos, design thinking e transformação digital).
Conheça nosso catálogo aqui.
Também fazemos oficinas presenciais e no formato remoto ao vivo, com dinâmicas, gamificação e testes individuais de auto avaliação. Conheça as oficinas aqui.
Temos flexibilidade para construir soluções de treinamento diferenciadas para cada empresa. Entre em contato aqui para saber mais.